本题可以结合几何直观来解释,在平面直角坐标系中构建一个梯形,可见F(0)和F(2)分别是梯形的上底和下底,和除以2为梯形中位线,因此只要证明F(1)短于梯形中位线即可,也就是证明F(X)是凹函数。当X小于1时,F(X)的导数小于○,当X大于1时,F(X)的导数小于0,因此,曲线形状是先单调下降经过1点达到最小值,然后再单调上升,1点为驻点。
| 笑话军事旅游美容女性百态母婴家电游戏互联网财经美女干货家饰健康探索资源娱乐学院 数码美食景区养生手机购车首饰美妆装修情感篇厨房科普动物植物编程百科知道汽车珠宝 健康评测品位娱乐居家情感星座服饰美体奢侈品美容达人亲子图库折扣生活美食花嫁风景 | 首页 |
对于R上可导的任意函数f(x),若x不等于1恒满足(x-1)f'(x)>0,证明f(0)+f(2)>2f(1)
小贴士:① 若网友所发内容与教科书相悖,请以教科书为准;② 若网友所发内容与科学常识、官方权威机构相悖,请以后者为准;③ 若网友所发内容不正确或者违背公序良俗,右下举报/纠错。
免责声明:本文为网络用户发布,其观点仅代表作者个人观点,与本站无关,本站仅提供信息存储服务。文中陈述内容未经本站证实,其真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考,并请自行核实相关内容。
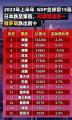 2023年上半年GDP全球前十五强
2023年上半年GDP全球前十五强百态 2023-10-24
美众议院议长启动对拜登的弹劾调查
百态 2023-09-13
百态 2023-09-13
探索 2023-09-06
印度或要将国名改为“巴拉特”
百态 2023-09-06
百态 2023-09-06
百态 2023-08-20
干货 2023-08-06
百态 2023-08-04
百态 2023-07-31
百态 2023-07-25
探索 2023-07-21
探索 2023-07-09
探索 2023-07-02
百态 2020-08-20
美国5月9日最新疫情:美国确诊人数突破131万
百态 2020-05-09
百态 2020-05-09
荷兰政府宣布将集体辞职
干货 2020-04-30
干货 2020-04-30
倩女幽魂手游师徒任务情义春秋猜成语答案逍遥观:鹏程万里
干货 2019-11-12
干货 2019-11-12
倩女幽魂手游师徒任务情义春秋猜成语答案神机营:射石饮羽
干货 2019-11-12
干货 2019-11-12
倩女幽魂手游师徒任务情义春秋猜成语答案昆仑山:拔刀相助
干货 2019-11-12
干货 2019-11-12
倩女幽魂手游师徒任务情义春秋猜成语答案天工阁:鬼斧神工
干货 2019-11-12
干货 2019-11-12
倩女幽魂手游师徒任务情义春秋猜成语答案丝路古道:单枪匹马
干货 2019-11-12
干货 2019-11-12
倩女幽魂手游师徒任务情义春秋猜成语答案镇郊荒野:与虎谋皮
干货 2019-11-12
干货 2019-11-12
倩女幽魂手游师徒任务情义春秋猜成语答案镇郊荒野:李代桃僵
干货 2019-11-12
干货 2019-11-12
倩女幽魂手游师徒任务情义春秋猜成语答案镇郊荒野:指鹿为马
干货 2019-11-12
干货 2019-11-12
倩女幽魂手游师徒任务情义春秋猜成语答案金陵:小鸟依人
干货 2019-11-12
干货 2019-11-12
倩女幽魂手游师徒任务情义春秋猜成语答案金陵:千金买邻
干货 2019-11-12
干货 2019-11-12
靜靜地坐在廢墟上,四周的荒凉一望無際,忽然覺得,淒涼也很美






